Cómo calcular varianzas
Contenido del Artículo
La varianza es una medida aritmética que nos permite conocer la dispersión que existe en un conjunto de datos. Matemáticamente hablando, la varianza es la media aritmética del cuadrado de las desviaciones respecto a la media de cierta distribución estadística.
Viene representada por el símbolo σ², que es la letra griega sigma en minúscula elevada al cuadrado, por lo que es una unidad de medida al cuadrado. Si deseas conocer la desviación estándar sólo deberás calcular la raíz cuadrada de la varianza.
Los resultados de la varianza nos dirán si los valores del conjunto estudiado están agrupados, cerca o dispersos. Un resultado pequeño indica que los valores están bastante agrupados, y en cambio, si el resultado de la varianza es grande, significa que los datos están dispersos.
Su uso es muy amplio estadísticamente hablando, por ejemplo, comparando la varianza de dos conjuntos de valores, por ejemplo femeninos y masculinos, se puede saber si una variable tiene un efecto destacable. Por otro lado, si estás creando un modelo estadístico la varianza puede indicar que estás ajustando mucho los datos.
A continuación te mostramos cómo calcular la varianza.
Tipos de varianzas
Podemos calcular la varianza muestral, es decir, cuando tenemos una población extremadamente grande, cogeremos una muestra y de ahí se estimarán los resultados.
La varianza de la población es el cálculo de la varianza d el total de la población. Se calcula usando todos los datos de la población de estudio.
La varianza de datos agrupados es otro caso en el que calcularemos la varianza cuando los datos de estudios están agrupados en diversas categorías o en grupos.
Propiedades de la varianza
- El valor de la varianza siempre será igual o mayor que cero.
- Si se le suma un mismo número a todos los valores de la variable que tenemos en cuenta, la varianza permanece igual.
- Si se multiplican todos los valores de la variable por un mismo número, entonces la varianza resultará multiplicada por el cuadrado de ese número utilizado.
- Si disponemos de diversas distribuciones que poseen la misma media y si sabemos sus varianzas, podremos calcular la varianza total.
Datos sobre la varianza
- La varianza es muy sensible a los valores extremos, al igual que la media, por lo que si tenemos valores muy extremos la varianza puede no ser del todo fiable.
- Si no podemos calcular la media de una distribución, entonces tampoco podremos calcular la varianza de dicha distribución.
- Las desviaciones resultan al cuadrado, por lo que la varianza no usa la misma unidad que los datos utilizados en su cálculo.
Calcular las varianzas muestral
Xᵢ= cada dato de la distribución.
![]() = media aritmética de la distribución (sumaremos todos los valores de la distribución y dividiremos el resultado por la cantidad de datos que tenemos).
= media aritmética de la distribución (sumaremos todos los valores de la distribución y dividiremos el resultado por la cantidad de datos que tenemos).
N= número de valores que tenemos en la distribución muestral.
Para calcular la varianza muestral nos proporcionarán algunos valores de todo el conjunto poblacional. Digamos por ejemplo que tenemos la siguiente distribución:
9, 8, 6, 5, 3, 2
Para calcular la varianza de esta distribución comenzaremos calculando su media:

Calcular las varianzas de la población
En este caso el proceso sería completamente igual que el anterior, lo único es que varían los símbolos que usaremos en la fórmula y que usaremos todos los datos que componen la población, por lo que el resultado de la varianza será exacto.
Primero: calcularemos la media de los datos de la distribución
Segundo: calculamos la suma de los cuadrados de las diferencias de los datos respecto a la media aritmética.
Por último: dividiremos el resultado entre el número de datos total que proporciona la población.
Calcular las varianzas de datos agrupados
Para calcular la varianza de datos agrupados partiremos de datos incluidos en grupos y la cantidad de veces que se repite un dato en el grupo.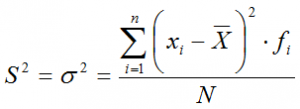
Por ejemplo, partiremos de estos datos:
Li= valor inferior
Ls= valor superior
Xi= Marca de clase – valor medio calculados con los datos inferiores y superiores.
Fi= frecuencias (cantidad de veces que se repiten los datos en el grupo)
N= es la suma de todas las frecuencias
n-1= suma de frecuencias menos . (usaremos este dato en vez de n cuando calculamos la varianza de datos agrupados de una muestra).
Con este ejemplo calcularemos la varianza poblacional para varios grupos de salarios y los números de trabajadores que hay en cada grupo.
| salarios Li | salarios Ls | fi -nº trabajadores | Xi | Xi*fi |
| 100 | 200 | 12 | 150 | 1800 |
| 200 | 300 | 10 | 250 | 2500 |
| 300 | 400 | 15 | 350 | 5250 |
| 400 | 500 | 18 | 450 | 8100 |
| 55 | 17650 |
Primero: calcularemos la marca de clase
Segundo: calcularemos Xi*fi
Tercero: con estos datos calculamos el promedio
Media= 17650/55=320.91
A continuación calcularemos la varianza:
| Xᵢ – |
(Xᵢ – |
(Xᵢ – |
| -170,91 | 29209,92 | 350519,01 |
| -70,91 | 5028,10 | 50280,99 |
| 29,09 | 846,28 | 12694,21 |
| 129,09 | 16664,46 | 299960,33 |
| 713454,545 |
Primero: calculamos Xᵢ – ![]()
Segundo: el resultado lo elevamos al cuadrado
Tercero: el resultado lo multiplicamos por fᵢ
Cuarto: Sumamos todos los resultados de todas las clases
Quinto: Dividimos el resultado anterior entre N
σ²= 713454.545/55=12971,90
Con estos sencillos pasos y ejemplos ahora ya sabrás cómo calcular la varianza de tus distribuciones de datos estadísticos.

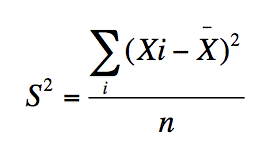


Creo que hay un error en las primeras 2 fórmulas, abajo dice N y creo que es n-1. Gracias, excelente página.
En la primera formula que se refiere a la varianza de la muestra abajo no va N, tiene que ir n-1. Mientras que, cuando se neceita calcular la varianza poblacional es correcto tener N abajo
En el ejercicio sobre salarios, como se aplican los resultados de forma practica para corregir posibles dispersiones respecto al salario promedio?
alguien me podría decir cuando usar la formula para VARIANZA DE DATOS AGRUPADOS Y NO AGRUPADOS… por favor
Muy buena pagina
Hola.
Un trabajador que tenga un ingreso correspondiente al límite superior de una clase, por ejemplo 200 unidades monetarias, en cuàl clase queda incluído en la primera clase o en la segunda, que también tiene a 200 como límite inferior de la clase subsiguiente. Agradezco su respuesta por favor.
Como calculo el punto de pedido necesario para un almacén de lavadoras, si el nivel de servicio que se quiere lograr es del 95% (k=1,64). Este artículo posee una demanda de 400 aparatos al mes, con un varianza de 100. Además se sabe que el proveedor se demora unas 5 semanas en poner a disposición la mercancía. Y calculo también el stock de seguridad
Gracias
Pues lo único en lo que tengo duda es de como sacaron
_
X