Cuál es la diferencia entre circunferencia y círculo
Contenido del Artículo
Es muy común confundir estos dos conceptos: circunferencia y círculo. Si bien ambos están muy relacionados la diferencia entre ellos es muy grande. Son dos conceptos geométricos que se relacionan pero que no deben confundirse.
Ambos tienen en común la forma redonda que todos conocemos. A grandes rasgos podríamos decir que la circunferencia hace referencia al “borde” en cambio el círculo es el “borde más el interior”.
La rigurosidad de la Matemática y por ende de la Geometría no permite definir así no más sus objetos de estudio. Por ejemplo cuando hablamos de algo redondo y plano inmediatamente lo relacionamos con el círculo, esto sirve únicamente para ejemplificar con algo concreto un objeto matemático para que un niño lo entienda. La realidad es que los objetos matemáticos o geométricos son “ideales” no “concretos” por lo que cuando damos un ejemplo y los relacionamos con cosas reales debemos tener en cuenta que ese objeto no es un círculo o una circunferencia o un cuadrado, simplemente es algo que se parece al verdadero círculo o circunferencia o cuadrado que son objetos que sólo existen en la mente.
Cuando los dibujamos una circunferencia o un círculo o un cuadrado, por ejemplo, estamos haciendo una representación en el plano de ese objeto ideal. Cuando decimos que ese tarro de tomates es un cilindro deberíamos decir que ese tarro de tomates tiene forma de cilindro, no es un cilindro. Esto es la rigurosidad matemática.
Ahora te mostraremos cuál es la diferencia entre circunferencia y círculo.
Que Necesitas
- Reconocer la diferencia entre estos dos conceptos
- Relacionar circunferencia y círculo con perímetro y área.
- Lápiz, compás y papel para representarlos.
- Calculadora para calcular perímetros y áreas.
Instrucciones
- Tal como lo explicamos antes la circunferencia y el círculo son objetos matemáticos ideales, existen sólo en la mente de las personas pero debemos valernos de representaciones para poder llevarlos al plano del papel, a la tierra, al espacio o relacionarlos con objetos reales y concretos, que se pueden ver y tocar, para aprender sobre ellos, diferenciarlos, poder ejemplificar y hacer cálculos de áreas y perímetros.
- Ya los filósofos y matemáticos de la antigüedad discutían y se preocupaban por conocer cuál era la relación entre el círculo y su diámetro. Todos intentaban encontrar el por qué cuando dividían el contorno del circulo por su diámetro obtenían el mismo cociente, sin importar el tamaño del círculo. La relación contorno-diámetro era un número cercano a tres. Así surgió este número irracional que todos conocemos como el número Pi, en griego ∏

- Aclaremos algunos conceptos:
- Circunferencia: “Es el conjunto de infinitos puntos que equidistan de otro llamado centro”. Esto nos da la idea de que la circunferencia es sólo una línea de puntos, un contorno, un borde, en palabras simples es hueca.
- El radio de la circunferencia es la distancia desde el centro hasta uno de sus puntos (cualquiera ya que están todos a la misma distancia de él).
- El diámetro es la distancia entre dos de sus puntos pasando por el centro, en otras palabras el diámetro es el doble del radio o el radio es la mitad del diámetro.
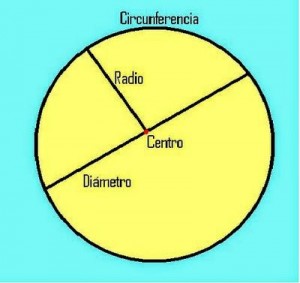
- El círculo es toda la superficie que encierra la circunferencia. También podemos decir que el contorno o borde del círculo es una circunferencia. El círculo, igual que la circunferencia tiene radio y diámetro.

- Finalmente veremos que podemos calcular de cada uno:perímetro o área?
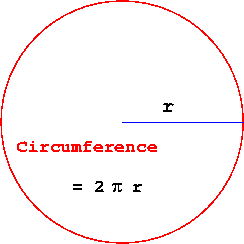
- Si nos referimos a una circunferencia únicamente podremos calcular su perímetro o contorno ya que en su interior no hay nada por lo que sería imposible calcular área (recuerda que el área implica una superficie plana y la circunferencia no tiene). En el perímetro de la circunferencia interviene el diametro (D) o el radio (r) y el número Pi: Perímetro = ∏. D o bien Perímetro = 2. ∏. r
- En el área del círculo intervienen el número ∏ y el radio: Área = ∏. r2

Consejos
- Cuando tengas que calcular perímetros y áreas debes tener bien claro que el perímetro hace referencia al borde o contorno, en cambio el área al interior de la figura geométrica, por ejemplo es imposible calcular el área de la circunferencia.
- Acostúmbrate a llamar las cosas por su nombre correcto, a comparar, diferenciar para reconocer y nombrar con exactitud los nombres de los objetos de la Geometría, como en este caso circunferencia y círculo.







Buenos tips y ejemplos que te dan ayuda a salir adelante en tus dudas. Gracias
Celenticima santidad no quiero que piense que quiero aprovecharme de algo por que haci me ciento . Pido que por favor me escuche ya que no beo inicios que se me solucione mi cicituacion en canarias fuerteventura . Pido vivir en un hogar ya que luchó por el ya hace unos años y me des quitan mi situación . Soy madre de 2 hijos una hija de 21 y un hijo de 15 niños con asma gronicos pulmonar y riñón perbis mi hija y mi hijo asmático y alérgico y no se me escucha mi decesperacion por mis hijos yo estoy en fermento pero yo no cuento ya que solo quiero tener un hogar y poder como cualquier familia vivir y disfrutar de mis hijos solo pido eso sufro costanera mente por ello y no veo a qui que me lo solucionen cuando todos tienen un hogar dijno como ellos que tienen todo solucionado y se olvidad de la cituación de quien lo nececita un abrazo enorme espero su repuesta gracias
muchas gracias por los consejos me ayudaron mucho
como te corespode
Muy buena explicación y ejemplos ,muchas gracias.
Gracias me aclararon mis dudas.
Me uyudaro a salir de muchas dudas genial informacion
muy buena esplicacion gracias
gracias por darme este tema era para un trabajo de mi escuela
Me gustó