Cómo calcular la desviación típica
La desviación típica es una de las fórmulas más conocidas en las matemáticas de hoy en día, una fórmula que nos va a permitir calcular muy fácilmente lo que se ha desviado un producto de la media.
Esto pertenece a las matemáticas de estadística, unas matemáticas que se encargan de analizar todos los datos con objetivos de clasificación y análisis. La desviación típica se encarga de decirte exactamente la relación con la media de los productos, viendo lo que se suele desviar de lo que es la tendencia.
A más desviación típica haya, más extremos tendremos, ya que hay más desviación típica cuando tenemos datos del 1 al 20 que cuando los tenemos del 1 al 10.
Eso si, lo malo de la desviación típica es que se las trae, ya que aunque la fórmula sea sencilla, hay que calcular antes otras cosas que no lo son tanto, como la marca de clase y la varianza, las cuales tienen fórmulas largas.
Hoy te vamos a enseñar como calcular todo esto, es decir, que hoy aprenderás a hacer varianza, marca de clase, desviación típica y coeficiente de variación, todo al completo. Además vas a tener un ejercicio resuelto para poder resolver todas tus dudas fácilmente.
Instrucciones para calcular la desviación típica
- Calcular la media de los datos:
Lo primero que debemos hacer para poder calcular la desviación típica de la manera correcta es calcular la media de los datos. La media de los datos no es más que tratar de llegar a un punto medio entre todo lo que hay. Si por ejemplo hay dos personas, uno que mide 1,50 y otro que mide 1,60, la media será 1,55, que es el punto medio entre los dos. La forma de calcularla es fácil, ya que sumas todos y divides por el número de gente que hay o de datos que hay. Sin embargo, en este caso se complica un poco, ya que a veces no nos dan datos exactos, sino que nos dan datos por intervalos, los cuales se deben sacar por la llamada marca de clase.- Calcular la marca de clase si tenemos datos separados: Si por ejemplo tenemos que el ejercicio nos da intervalos en vez de datos reales, es decir, que en vez de decirme que Jaime mide 2,03 nos dice que mide entre 2 y 2,05 metros, debemos calcular la marca de clase. Esto es una media entre los dos valores y se calcula de la misma forma que la media normal, así que seguramente la sepas hacer sin ningún tipo de problema.Por ejemplo si tenemos gente de entre 2 y 4 años, la marca de clase es 3. Esto nos permitirá sin lugar a dudas resolver cualquier tipo de problema de desviación típica, ya que lo único que hay que hacer para resolverlos es ir haciendo la marca de clase de todos los valores y dejarlo como un valor real con el que después hay que hacer la media.

- Calcular la marca de clase si tenemos datos separados: Si por ejemplo tenemos que el ejercicio nos da intervalos en vez de datos reales, es decir, que en vez de decirme que Jaime mide 2,03 nos dice que mide entre 2 y 2,05 metros, debemos calcular la marca de clase. Esto es una media entre los dos valores y se calcula de la misma forma que la media normal, así que seguramente la sepas hacer sin ningún tipo de problema.Por ejemplo si tenemos gente de entre 2 y 4 años, la marca de clase es 3. Esto nos permitirá sin lugar a dudas resolver cualquier tipo de problema de desviación típica, ya que lo único que hay que hacer para resolverlos es ir haciendo la marca de clase de todos los valores y dejarlo como un valor real con el que después hay que hacer la media.
- Varianza;
La fórmula más importante del ejercicio, es la desviación típica, sin embargo, no hay desviación típica si no tenemos varianza, así que tenemos que aprender antes de nada a calcularla de la manera correcta. La fórmula es exactamente así:Sumatorio de marca de clase menos la media de los datos al cuadrado por el número de datos que se corresponden por cada dato(f sub i) partido del número de datos que se cogen(n). Aquí hay que ir restando la marca de clase menos la media que hemos calculado antes. Una vez que la tengamos, vamos a hacer el cuadrado(sino podría quedar negativo) y multiplicamos cada uno por cada frecuencia de cada dato. Lo sumamos todo(son sumatorios) y lo dividimos entre el número de datos que hay. Se que es un poco complicado ahora de entender, sin embargo, luego te presentaré un ejemplo, ejemplo que te va a permitir que entiendas esto enseguida. - Fórmula de la desviación típica:
Ahora es el turno de calcular la desviación típica, ya que es para lo que estamos aquí y es la fórmula más importante de todo el ejercicio, sin lugar a dudas. La desviación típica es la raíz de la varianza, ni más ni menos,. Una raíz cuadrada es lo contrario a un número cuadrado y se hace fácilmente con cualquier calculadora, en la cual pulsaremos en el icono de raíz cuadrada que todo el mundo conoce y que calculara de manera automática esa raíz. Una vez que la hayamos hecho, sólo queda apuntar en un papel la desviación que nos ha salido, algo que nos dirá que ya tenemos el ejercicio totalmente acabado y listo para entregar.
- Coeficiente de varianza:
Eso si, hay profesores que van a ir un poco más allá, ya que no sólo nos va a pedir, la desviación típica, sino que nos va a pedir el llamado coeficiente de varianza. Este coeficiente no es más que un porcentaje sobre la varianza y la media de los datos, el cual nos va a decir la cantidad en la cual estos varía. Esto se calcula haciendo la fórmula de Desviación típica entre media de X. Esto nos da un número que siempre tiene que ser menor a uno, ya que sino algo estaríamos haciendo mal. La gente suele expresarlo multiplicado por 100 para poderlo expresar un tanto por ciento, ya que es como se debe de entregar y como mejor funciona para los profesores, aparte de que lleva un segundo hacer el tanto por ciento y queda siempre muchísimo mejor que poner decimales. - Ejercicio con ejemplo:
Enunciado: Tenemos 10 personas en una clase, de las cuales una tiene entre 1 y 2 euros, 3 personas tienen entre 3 y 4 euros, 5 tienen entre 4 y 5 euros y 1 tiene entre 6 y 7 euros. Calcula la desviación típica y el coeficiente de variación:
Lo primero que debemos hacer es hacer la media de los datos, algo que sólo podremos hacer calculando las respectivas marcas de clase de los euros. Lo he puesto fácil para que todas salgan bien, ya que la primera es 1,5(1+2/2), la segunda es 3,5, la tercera es 4,5 y la cuarta es 6,5. Luego ya podremos hacer la media multiplicando cada una por el número de gente que hay, saliendo 1,5 la primera, 10,5 la segunda, 22,5 la tercera y 6,5 la cuarta, saliendo un total de 41/10 y 4,1 euros de media. Una vez que ya tenemos la media, hay que pasar a calcular la varianza, algo que vamos a poder hacer restando la media a cada marca de clase primero. En la primera sale -2,6, la segunda sale .0,6, la tercera sale 0,1 y la cuarta sale 2,4. Todo esto lo hacemos un cuadrado, lo cual nos sale 6,76 la primera, 0,36 la segunda, 0,01 la tercera y 5,76 la cuarta y última. Ahora hay que multiplicar por el número de personas que tienen este dinero, saliendo en la primera 6,76(1 persona), en la segunda 1,08, en la tercera 0,05 y en la cuarta 5,76. Todo esto lo sumamos y nos da 13,65, lo cual lo tenemos que dividir entre 10 personas que hay en clase, saliéndonos la varianza 1,365. Si queremos la desviación típica, debemos hacer la raíz de esto, la cual es 1,168 aproximadamente.El coeficiente de variación va a ser 1,168(desviación típica) entre la media que va a ser 4,1. Esto da 0,28, lo cual si lo multiplicas por 100 da un 28% por ciento. Como puedes ver, el ejercicio es simple, sólo que es muy complicado explicarlo con palabras, sin embargo, viéndolo en un papel es muchísimo más sencillo.
- Representaciones gráficas:
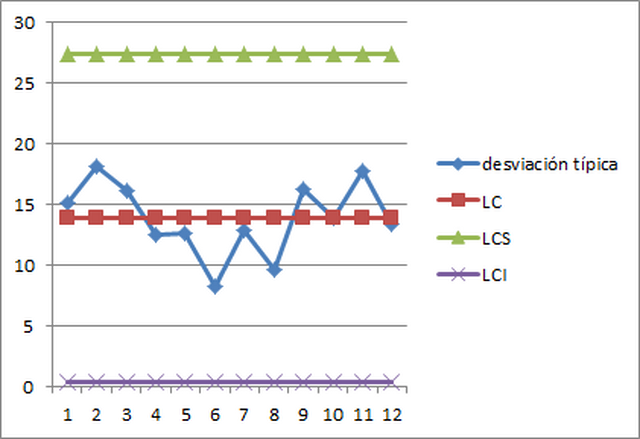
Si te lo pide o si simplemente le quieres dar un pequeño toque de calidad al ejercicio, puedes optar por las representaciones gráficas, las cuales sirven para expresar varias cosas del ejercicio. Puedes trazar una gráfica en la cual cada marca de clase sea la X y la frecuencia sea la Y. Traza una línea que lo represente y después trata de expresar allí datos como la media(la cual suele estar cerca del medio) y otros datos. Si te fijas, seguramente te hayas salido la famosa campana de Gauss(que por cierto estaba en todas partes, porque no paro de escuchar su nombre), la cual sale cuando hay poca frecuencia de valores bajos, alta frecuencia de valores medios y baja frecuencia de valores altos. Esto ocurre ahora mismo en la población Española, ya que hay pocos jubilados, pocos jóvenes y mucha gente adulta. Sin embargo, esto va a cambiar y seguramente acabe siendo una pirámide invertida. En definitiva, la representación gráfica nos va a servir para poder ver mejor cual es la media y a llevar mejor el ejercicio a la práctica y a la vida real.
Consejos para calcular la desviación típica
- Aprender el ejercicio mejor:
Este ejemplo que te he puesto te puede servir para empezar a entenderlo, sin embargo, puede ser que todavía tengas tus pequeñas dudas, ya que es perfectamente normal en este mundillo. Lo que tienes que hacer es tratar de aprender el ejercicio de la forma correcta, viendo el enunciado y después haciéndolo tu de la manera correcta, poniendo el enunciado en un papel, con todos los datos claros y después tratando de hacerlo tu mismo, sin ayuda de nadie y en un papel. También puedes buscar en internet enunciados de la desviación típica, ya que hay miles de millones de ejercicios en el mundo que te permitirán poder mantener todo esto de una forma muy sencilla y poder hacer ejercicios de estos a saco, hasta que puedas conseguir mucha soltura aquí. - Aprender más matemáticas:
En esta sección de educar tenemos buenas noticias para ti, ya que vamos a aprender matemáticas de todas las formas posibles. en primer lugar, vamos a tener matemáticas de estadísticas, es decir,matemáticas que te van a servir para calcular datos, trabajar con gráficas y demás. También tenemos otras matemáticas, como por ejemplo ingenierías, las cuales te sirven para aprender cosas más avanzadas. Sin duda , te merece la pena visitar todos estos artículos, ya que en el fondo vas a poder encontrar fácilmente todo esto y mucho más sin tener que salir de aquí. - Comentarios con dudas:
Si tienes alguna duda sobre cómo hacer la desviación típica, debes tener en cuenta que es algo normal, sin embargo, no pasa nada, ya que nosotros estamos aquí para resolver todas tus dudas sin ningún tipo de problemas. Si quieres que resolvamos los expertos de doncomos tus dudas, deja tu comentario abajo, ya que si lo haces, te vamos a poder ayudar a que lo resuelvas y que puedas tener el ejercicio perfecto. Deja cualquier cosa, aunque te parezca una tontería, ya que somos humanos y es normal tener errores. Lo que hay que hacer es tratar de resolverlos lo antes posible y para eso estamos nosotros aquí.


Me parece que la forma didactica deberia ser mas explicita o bien ir paso a paso para hacerlo mas facil de explicar, de tal manera pues que de alguna manera se pueda aprender para siempre lo señalado y no que sea un pasatiempo o bien un analisis circunstancial o de exigencia de una catedra,.
Explicación sencilla y con ejemplos. Así da gusto…
Gracias
si en un ejercicio me dan la media arismetica y la media geometrica como se debe hacer
Halle la desviación típica de dos números cuya media aritmética es 9,0 y su media geométrica es 7,2.