Cómo multiplicar fracciones
Contenido del Artículo
Si te has preguntado cómo multiplicar fracciones, te decimos que es un procedimiento sumamente sencillo, sólo se necesita de unos cuantos pasos de los que hablaremos más adelante; primero miremos un poco sobre las fracciones como tal.
Historia de los Números Fraccionarios
Como se sabe, los primeros números que construyeron fueron aquellos que llamamos naturales, aquellos que nos sirven para contar cantidades, que como su nombre mismo lo dice, son naturales, por naturaleza, por ejemplo: veinte personas, cinco caballos, tres casas, treinta lapiceros, dos mariposas, cuarenta campanas, tres mulas, cinco muñecos, entre otros; esto entonces le servía a los antiguos para contar el ganado que poseían, a los miembros que conformaban la familia y claro está para los bienes que tenían e intercambiaban.
A medida que fue pasando el tiempo se fueron dando cuenta que no sólo se necesitaba de los números naturales sino también de algo más, pues por ejemplo había media naranja, un cuarto de manzana o una calabaza y media y de esta manera los racionales surgieron. Los egipcios y los mesopotámicos ya trabajaban y utilizaban algunas fracciones sencillas como 1/5, 1/3, 1/2, entre otras, por lo general tenían al número UNO como denominador y muy de vez en cuanto utilizaban otros como el 2/5, pero lo más común era la fórmula 1/x.
Así entonteces, podemos decir que al parecer los egipcios fueron quienes por vez primera hicieron uso de las fracciones, claro que sólo eran las de la forma que se conocen como 1/x, o sea la que se obtiene como una combinación de ellas mismas, lo que quiere decir que los egipcios utilizaban las fracciones que tenían como numerador al número UNO y como denominador los números DOS, TRES, CUATRO, CINCO, aunque a veces sí utilizaban fracciones como ¾ o 2/3, pero no era común, logrando así poder hacer diversos cálculos de fraccionarios.
Podemos decir que en los papiros de Moscú y de Rhind, así como en la piedra roseta, encontramos registros de fraccionarios, estos pueden ser unos de los más antiguos, o se piensa que inclusive el más antiguo; los dos son provenientes de los egipcios y su cultura.
Entonces los antiguos trabajaban con racionales que eran realmente fraccionarios, ya que como su mismo nombre lo indica, los fraccionarios nos sirven para poder entender los fraccionamientos de algún objeto el cual es conocido. Pues el trabajo como tal de los racionales, como se nos ha explicado de la fórmula a/b donde a y b vienen a ser naturales y b viene a ser distinto a cero; se dio mucho después a esta cultura, alrededor del año 1500.
Los babilonios también por su parte desarrollaron un sistema bastante eficaz de notaciones fraccionarias, lo que les permitió establecer unas aproximaciones de tipo decimal, las cuales fueron en verdad sorprendentes. La evolución y la simplificación del método que utilizaban en los fraccionarios permitieron el origen de operaciones matemáticas nuevas, las cuales ayudaron a las mismas matemáticas que vendrían posteriormente (siglos después) y a su comunidad, pues gracias a esto ya se podían hacer excelentes cálculos entre los que encontramos por ejemplo una raíz cuadrada.
Para los babilonios era en cierta forma sencillo poder conseguir sus aproximaciones que resultaban ser bastante precisas; pues en sus cálculos procedían a utilizar notaciones de tipo fraccionario; esta civilización tuvo la mejor notación de fraccionarios hasta que llegó el renacimiento.
También hay que destacar acá a la China antigua, pues justo allí se dio aquel hecho donde ya se exige que en una división de fracciones haya una reducción de estas misma a un común denominador.
Los chinos antiguos conocían bastante bien las diferentes operaciones de las fracciones que son ordinarias, llegando al punto de que podían, en este contexto, hallar perfectamente lo que conocemos como el mínimo común denominador de las fracciones; estos a su vez adoptaron algunas añagazas con los decimales para poder acelerar un poco el proceso de las fracciones y su manipulación.
Este artículo también te puede interesar: Cómo Convertir Fracciones a Decimales
Los griegos tampoco se quedaron atrás y también debemos mencionarlos, pues éstos se destacaron ampliamente en la geometría y en construcciones que utilizaban a la misma, en estas últimas representaban sus longitudes con números racionales.
Concepto de una fracción
Si ya queremos saber en sí cual es el concepto de una fracción, es la que nos da una idea que es intuitiva, que nos ayuda a dividir la totalidad de algo en partes completamente iguales; por ejemplo cuando hablamos de la hora, estamos hablando de fracciones, mira que decimos, hora y cuarto o un cuarto de hora, media hora, entre otros; podemos decir que nos hemos comido la mitad de una tarta, o vamos a echar gasolina y solo queremos llenar hasta la mitad del tanque. Ya que te lo puedes estar preguntando, si los ¾ de una hora no vienen a ser lo mismo que los ¾ de una tarta, pero su cálculo sí es el mismo, pues lo que hacemos es dividir la totalidad ya sea de una hora o de una tarta en 4 partes exactamente iguales y luego tomando de esas partes 3.
La fracción está representada matemáticamente hablando, por unos números que se encuentran escritos sobre otros, y estos son separados por una raya horizontal que recibe el nombre de raya de fracción o fraccionaria, el número de arriba de la raya se llama numerador y el de abajo denominador.
Cómo se multiplican las fracciones
Ahora sí miremos cómo se multiplican los números fraccionarios.
Paso uno
Multiplica los dos números de arriba, éstos son llamados nominadores.
Paso dos
Multiplica los dos números de abajo, éstos son llamados denominadores.
Paso tres
Simplifica el número que te queda.
Miremos con un ejemplo
Cuando comiences a escribir el problema matemático de fracciones debes ver que los numeradores estén bien alineados con sus respectivos denominadores, como lo mostramos en las imágenes posteriores.
Paso uno
Multiplicaremos los números de arriba, los nominadores
4/5 X 5/3 = 4 X 5 = 20 entonces tenemos que 20 es el nominador que nos arroja el resultado.
En este caso los numeradores son el 4 y el 5, por eso son los que debes multiplicar para luego obtener el resultado de 20.
Miremos la ilustración a continuación
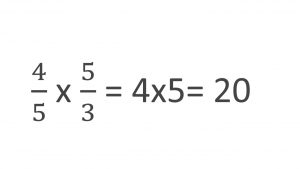
Paso dos
4/5 X 5/3 = 5 X 3 =15, entonces tenemos que 15 es el denominador que nos arroja el resultado
Los denominadores en este caso son el 5 y el 3, por lo cual son los que debes multiplicar para de esta forma obtener el número 15.
Así como en la siguiente ilustración
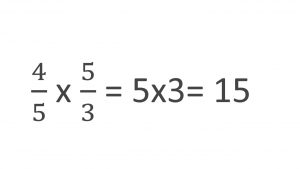
Paso tres
Entonces tenemos que nos queda un resultado de esta manera 20/15, o sea que nos ha arrojado un nominador y un denominador nuevo.
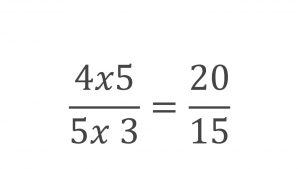
Paso cuatro
Ya tenemos un resultado pero esto no termina aquí, en este punto nos falta simplificarlo, para eso debemos hallar algo llamado MCD lo cual tiene el significado de Máximo Común de División que se da entre el numerador y el denominador; para esto buscamos el número más grande por el que cada uno se pueda dividir, así entonces si tenemos el número 20 y tenemos el 5 aplicaríamos dividirlo por 5, pues podemos dividir el 10 por 5 el cual nos dará 4 y podemos dividir el 15 por 5 el cual nos dará 3, mira que no se puede dividir en 2 porque nos daría un número decimal en el 15, tampoco por 3 porque pasaría lo mismo en el 20, por 4 nos pasaría en el 15, pero por 5 obtenemos el resultado tanto del nominador como del denominador en números naturales. Entonces tenemos que el MCD del nominador 20 y del denominar 15 es el número 5 y cuando simplifiquemos la fracción nos debe quedar 4/3 y listo, así obtienes el resultado de una multiplicación de fracciones.
Mira la ilustración
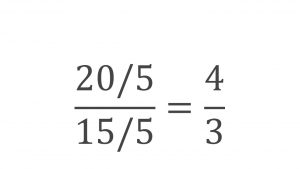
En palabras más sencillas, antes de simplificar debes dividir tanto el numerador como el denominador por un número entero, y debe ser el más grande que se pueda en ambos.
Otro método para multiplicar fracciones
Existe otro método que consiste en que simplifiquemos antes de que hagamos la respectiva multiplicación.
Paso uno
Igualmente el numerador debe estar alineado con el denominador.
Paso dos
Deberás simplificar la primera fracción de la misma forma que enseñamos anteriormente, mirando cual es el número más grande por el que se pueden dividir el numerador y el denominador.
Paso tres
Toma la segunda fracción y haz lo mismo, simplifícala buscando el número más grande por el que puedas dividir tanto el numerador como el denominador.
Paso cuatro
Multiplica los números que te quedaron después de simplificar la fracción que quieres multiplicar, como ya lo habíamos enseñado los numeradores y luego los denominadores y así obtendrás la respuesta; como simplificaste antes de multiplicar no tendrás que hacerlo con el resultado arrojado, sino que ese será el final; igual debes revisar el resultado porque si éste se puede simplificar lo deberás hacer.
Notas para tener en cuenta al momento de multiplicar fracciones.
- Recomendamos el primer método, es más sencillo
- Las fracciones simplificadas se deben continuar simplificando hasta que lleguen a una fracción que ya es irreducible, o sea que no se puede simplificar.
- Si vas a multiplicar alguna fracción por un número entero, deberás coger este último como nominador y pon de denominador el número 1, y ya puedes hacer la multiplicación igual a como te la enseñamos en este artículo.


este multiplicar con facciones educativo en este dia tan emocional de mi vida GRACIAS .