Cómo saber la pendiente de una recta
Contenido del Artículo
Saber cómo hallar o calcular la pendiente de una recta se puede aplicar en más ocasiones de lo que se piensa. Además, la pendiente de una recta es un conocimiento clave de la base de muchas materias. Por ejemplo, materias como álgebra, matemáticas aplicadas a las ciencias sociales, economía…
Saber la pendiente de una recta es un conocimiento que la gran mayoría adquiere en su paso por la escuela. Pero, como bien pasa muchas veces, estos conocimientos se suelen ir olvidando con el tiempo. O, también puede suceder que no nos enteremos bien de las explicaciones del profesor. O, que sea un concepto que se nos atraganta y no sepamos cómo resolverlo.
Aunque, por otra parte, la visión de una pendiente es constante en nuestro día a día. Lo que pasa es que seguramente no pensemos en ello cuando las vemos. Por ejemplo, podemos pensar en un coche bajando una rampa o una persona bajando las escaleras. De igual forma, podemos ver cómo sube un animal a una colina o cómo se escalan las montañas. Estos son ejemplos de lo presente que están las pendientes en nuestra vida.
Pues bien, en este artículo pretendemos enseñar las reglas básicas para saber calcular la pendiente de una recta.
Qué es una pendiente
Antes de saber cómo se calcula la pendiente de una recta, primero debemos saber y comprender qué es una recta en sí. Una pendiente se conoce en matemáticas y ciencias de aplicaciones sociales como la inclinación de un elemento ideal, tanto natural como constructivo respecto de una línea recta horizontal. En palabras más técnicas, la pendiente de una recta es la tangente del ángulo que da lugar la recta con la dirección del eje X (o eje de abscisas).
Toda esta información puede llegar a resultar muy confusa al principio. Por eso, una pendiente podemos definirla de una forma más coloquial y sencilla. Podemos decir que una pendiente es la trasformación que tiene lugar en el eje Y (o el eje de ordenadas), divido entre la trasformación que sufre el eje X (o eje de abscisas).
Antes de saber cómo se halla la pendiente de una recta, tenemos que saber algo. Y es que es algo fundamental para el fin de este ejercicio. Para poder saber una pendiente, las líneas tienen que ser rectas. No podemos averiguar la pendiente de una recta si la línea es curva. Parece obvio si miramos el nombre del ejercicio, pero muchas veces, cuanto más claro parece que es algo, menos lo entendemos.
Características de una pendiente
Por otra parte, cabe pensar que la recta, según su inclinación, puede ir hacia arriba o hacia abajo. O, prestando atención a los nombres técnicos, la pendiente de una recta puede ser tanto positiva, como negativa. Como vemos, existen varios tipos de recta.Cuando una recta se representa gráficamente, es mucho más sencillo determinar qué tipo de pendiente es. Ya que la inclinación de la pendiente es la que identifica si es positiva o negativa.
Pendiente de una recta positiva
Decimos que una pendiente es positiva cuando la recta es creciente. Esto significa que comienza en un punto bajo para ir ascendiendo conforme se inclina. En otras palabras, podemos hablar de una pendiente positiva cuando al aumentar los valores de x, también aumentan los valores de y.
Pendiente de una recta negativa
Contrariamente al caso que acabamos de ver, hablamos de una pendiente negativa cuando la recta es decreciente. Es decir, que comienza en un punto alto de la gráfica y va descendiendo a medida que avanza por el gráfico. Podemos decir, de otra forma, que una pendiente es negativa si cuando se aumentan los valores de x, descienden los valores de y.
Pendiente de una recta nula
El último caso que se puede dar es este, que la pendiente de una recta sea absolutamente nula. Como podemos imaginar, la pendiente con valor cero se trata de una recta horizontal. O lo que es lo mismo, esta pendiente no tiene inclinación.

Cómo saber la pendiente de una recta
Para calcular la pendiente de una recta, os recomendamos que os hagáis con papel y lápiz. Podemos hacer nuestro propio gráfico para ver de una forma mucho más clara, la forma de calcular la pendiente. Esto lo podemos hacer sobretodo al principio, que es más probable que nos cueste entenderlo si aún no tenemos práctica.
De todas formas, se puede sacar la pendiente de una recta sin gráfico. Pero para ello es obligatorio que sepamos dos coordenadas de la recta que pretendemos calcular. Cada coordenada corresponde a un punto específico de la recta. De cada punto de la recta, podemos obtener dos coordenadas. Una para el valor X, que nos indica dónde se encuentra ese punto respecto al eje horizontal. Por otra parte, también obtendremos la coordenada para el valor Y, que nos aclara dónde esta ese punto respecto al eje vertical.
Dibujamos un gráfico y la recta
El primer paso que vamos a dar para calcular la pendiente de una recta es dibujar el gráfico que nos hará de guía. Para hacerlo, tendremos que hacer dos líneas perpendiculares entre sí. Para que te sea más fácil entenderlo, debes hacer dos líneas que se crucen en el centro, como si de una cruz se tratara. Ahora podremos ver que tenemos cuatro cuadrantes en total.
El primer cuadrante I, es el que corresponde al cuadrado superior derecho. El segundo cuadrante II, corresponde al cuadrado de la parte superior izquierda. A continuación, el tercer cuadrante III, se sitúa en el cuadrado inferior izquierdo. Por último, el cuarto cuadrante IV, es el que está en el cuadrado inferior derecho.
Ahora ya tenemos hecho el gráfico y, además, podemos contrastar la información anterior sobre la inclinación de las rectas y ver cómo sería una recta con pendiente positiva, con pendiente negativa o nula. Lo único que nos queda por hacer es dibujar la recta de la que después tendremos que calcular su pendiente. Podemos hacer la recta como queramos, tanto ascendente como descendente. Lo único que no podemos hacer es una recta nula. Porque, como es lógico, si la recta es nula no tiene inclinación, y si no tiene inclinación, no existe pendiente que calcular.
Lo importante a la hora de hacer la recta es que se haga con regla, para que sea efectivamente recta y no tenga ninguna ondulación.
Calcular la pendiente de nuestra recta
Ahora ha llegado el momento de calcular la pendiente de la recta que acabamos de dibujar. El primer paso que debemos dar es seleccionar los dos puntos que necesitamos en la recta. Da igual a que altura de la recta se encuentren los dos puntos. Y no es importante en qué cuadrante se encuentren los puntos que has seleccionado.
Pues bien, una vez escogidos los puntos, debemos determinar las coordenadas de cada uno. Esto es muy sencillo, solo tenemos que ver el valor que tiene en el eje horizontal y en el eje vertical. No importa si los números son negativos. Ahora escoge uno de los puntos con sus coordenadas ya determinadas y le daremos el nombre de x1,y1. De esta forma, ese punto que hemos escogido será el de las coordenadas dominantes. Y el otro punto restante se nombrará con x2,y2. Hasta ahora todo ha sido muy sencillo, y lo mejor de todo es que seguirá siendo sencillo. Lo único que tenemos es aplicar la siguiente fórmula.
m= y2 – y1/ x2 – x1
En la ecuación, m es el nombre que se le asigna a la pendiente de una recta y los demás valores ya los hemos obtenido antes. Por tanto, solo queda aplicar la fórmula.
Ejemplo práctico
Ahora vamos a hacer un ejemplo práctico por si han quedado dudas, que se puedan resolver. En primer lugar dibujamos el gráfico y hacemos la recta. Nos tiene que quedar algo como esto:
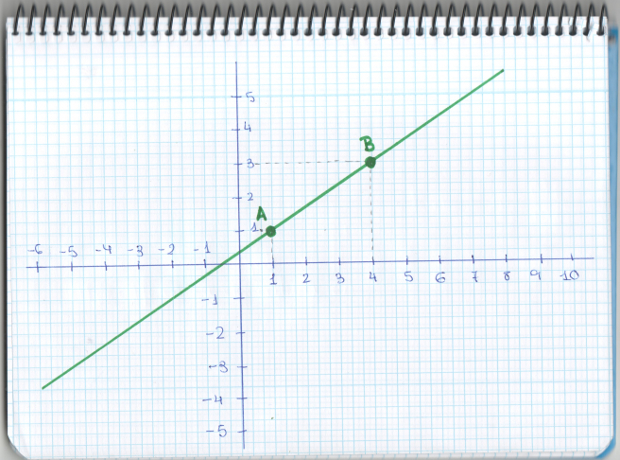
A continuación, escogemos dos puntos al azar, que serán diferentes a los del dibujo. En este caso, el primer punto se encuentra en el cuadrante III, con unas coordenadas de (-2, -3). Mientras que el segundo punto se sitúa en el cuadrante I, con unas coordenadas de (3,4). En el paréntesis, a la hora de poner las coordenadas, el primer número que se pone es el que se corresponde con el eje X. Por tanto, en el segundo lugar, se pone el valor del eje Y. Hemos escogido las coordenadas del cuadrante III como x1,y1 y las del cuadrante I como x2y2.
Ahora vamos a aplicar la fórmula. En este caso quedaría así: m= 4 – (-3)/ 3 – (-2). Primero, obtenemos el resultado del dividendo y del divisor a parte, sin hacer más cálculos. En nuestro caso quedaría así: m= 7/ 5. Por último, solo tenemos que calcular la división restante. Aquí nos daría un resultado de 1,4.
Por fin, podemos determinar que nuestra pendiente es de 1,4 y, además, podemos decir que tiene una pendiente positiva.

Como hemos visto, no ha resultado tan complicado determinar la pendiente de una recta. Siguiendo estos sencillos paso tenemos la forma de calcular la pendiente de cualquier recta. Esperamos que la información contenida en este artículo os haya servido de ayuda para resolver este problema matemático y que, de ahora en adelante, no haya pendiente que se os resista.

