Cómo hacer operaciones con fracciones
Contenido del Artículo
Una fracción es un número que nos indica de cuantas partes estamos hablando de un todo que ha sido dividido en ciertas partes iguales. El ejemplo más claro es cuando dividimos un pastel en 8 partes iguales, por ejemplo, y a nosotros nos ha tocado 1, en este caso estaríamos hablando de una octava parte o de 1/8.
Teniendo en cuenta cómo se escriben estos números, operar con ellos puede parecernos complicado, y la verdad es que no lo es, pero sí que requiere de ciertos conocimientos, y por supuesto de práctica para quedarnos bien con esta habilidad de operar con fracciones.
Si quieres aprender cómo hacer operaciones con fracciones sigue leyendo este artículo de doncomos.com donde vamos a enseñarte las principales operaciones que puedes hacer con fracciones, y cómo resolverlas adecuadamente.
Sumas y restas si las fracciones tienen el mismo denominador
La suma y restas de fracciones con el mismo denominador es el caso de sumas y restas más fáciles que podemos encontrar. En este caso solo tendremos que mantener el mismo denominador y sumar los numeradores. Y en el caso de la resta también vamos a mantener el mismo denominador y entonces restaremos los denominadores.
Ejemplo:
A / B + C / B= A+C / B
2/5 + 4/5= 2+ 4/5 = 6/5
Sumas y restas con distinto denominador
En el caso de que las fracciones tengan distinto denominador, las sumas y restas pueden llevarnos un poco más de tiempo, ya que para hacer la operación debemos calcular el común denominador.
Este denominador común se determinará calculando el mínimo común múltiplo de los denominadores.
El mínimo común múltiplo se calcula dividiendo los denominadores en sus divisores, y luego cogeremos, los comunes y no comunes con mayor exponente y se multiplicarán. El resultado de la multiplicación es el mínimo común múltiple.
Por ejemplo:
Mínimo común múltiple de 4 y 6
4= 2²
6 = 2, 3
m.c.m. (4,6)= 2² * 3 = 12
El paso siguiente consiste en cambiar todos los denominadores y poner el m.c.m. en su lugar. Y el numerador también cambiará. Deberemos dividir el m.c.m. entre el denominador de antes y luego, el cociente se multiplicará por el numerador, convirtiéndose este resultado en el nuevo numerador. Deberemos hacer esto con cada fracción.
Después realizaremos la suma o la resta como explicamos en el caso anterior de fracciones con el mismo denominador.
Ejemplo:
3 / 4 + 2 / 6 =
m.c.m. (4, 6)= 12
3/4 + 2/6= 9/12 + 4/12 = 13/12
Otra forma de calcular la suma o la resta de una fracción con distinto denominador, y quizás la forma más sencilla de lograrlo es a través de esta fórmula:
Multiplicaremos los dos denominadores, este será nuestro denominador común. Después, el cambio del numerador consistirá en multiplicar el numerador de una fracción con el denominador de la fracción de al lado.
La fracción final será múltiplo del resultado original, por tanto deberemos dividir tanto el numerador como el denominador por el mayor divisor común que tengan ambos números.
Ejemplo:
A / b + c / d= a*d +b*c / b*d
3/4 +2/6= 3*6+2*4 / 4*6 = 18+8 / 24 = 26 / 24 el cual es un múltiplo del resultado real, por lo que después deberemos dividirlo entre el mayor divisor común que tengan. En este caso, 2.
26: 2 / 24:2 = 13/ 12
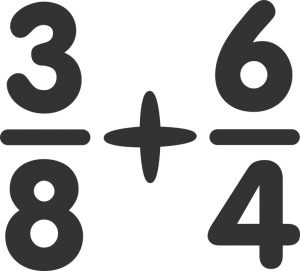
Multiplicación de fracciones
Aunque se crea lo contrario, la multiplicación de fracciones es mucho más sencillo que las sumas y las restas, ya que no hay que buscar un común denominador. En este caso solo tendremos que multiplicar numerador con numerador, siendo el resultado del numerador de la multiplicación y también multiplicaremos el denominador por el denominador, siendo el denominador final.
Ejemplo:
A / b * c/ d = a*c / b*d
3/4 * 2/6 = 3*2 / 4*6 = 6 / 24
Como ves, el resultado final es otra fracción, cuyo numerador es el resultado de multiplicar los numeradores de la operación, mientras que el denominador es el resultado de multiplicar los denominadores e la operación.
División de fracciones
Debemos tener en cuenta que para hacer una división de fracciones no tendremos que “dividir” como debe hacerse realmente. Realizar una operación de fracciones conlleva a multiplicar varias partes según un patrón. Que se conoce como:
El numerador final es el resultado de multiplicar los extremos, mientras que el denominador final será el resultado de multiplicar los medios. Ahora veremos un ejemplo con letras para que lo entendáis mejor.
Ejemplo:
A / b : c /d= a*d / b*c
3/4 : 2/6= 3*6 / 4*2 = 18 / 8

En las operaciones con fracciones es frecuente que el resultado se simplifique lo máximo posible, de ahí que debamos dividir el numerador y el denominador de la fracción final entre el mayor divisor común de ambos comunes y seguir dividiendo entre los divisores comunes hasta llegar al menor y por último obtener una fracción que no pueda simplificarse más al no tener más divisores comunes ambos números.
Operaciones con fracciones en la calculadora
Si deseas resolver tus operaciones con fracciones con la ayuda de la calculadora es bastante sencillo, y no tienes que recurrir a botones especiales. Tan solo deberás poner cada fracción entre paréntesis, dejando el símbolo de la operación fuera, entre paréntesis cerrado y paréntesis abierto. La barra de la fracción vendrá representada por el símbolo de la división. El problema de hacer esto con la calculadora es que el resultado te lo dará en números enteros o con decimales, y no en forma de fracción.
Si deseas introducir fracciones propiamente dicha en tu calculadora necesitarás una calculadora científica. En este caso será importante el botón con el símbolo de una fracción impropia: a b/c.
En este caso debemos pulsar este botón para introducir a continuación el número del numerador, volver a pulsar ese botón e introducir el número del denominador.
Por ejemplo: si queremos introducir 3/ 4, sería así: 3 botón a b/c 4
En el caso de que se trabaje con fracciones impropias, primero introducimos el número entero y luego la fracción como hemos hecho en el párrafo anterior.
Ejemplo: si queremos introducir 5 ¾, sería así: 5 botón a b/c 3 botón a b/c 4
A continuación vamos a ver un ejemplo cómo introduciríamos una operación con fracciones en la calculadora. Todas las operaciones se introducen igual, exceptuando que cambiamos el símbolo de la operación por el que corresponda en cada caso.
Ejemplo: 5 3/4 + 2/6
En este caso los botones son así: 5 botón a b/c 3 botón a b/c 4 botón a b/c símbolo (+, -, *, /) 2 botón a b/c 6
Esperamos que con esta explicación, y estos ejemplos hayamos podido resolver tus dudas sobre cómo hacer operaciones con fracciones. Recuerda que esto no es tan complicado como puedes llegar a pensar, pero sí que es importante que practiques mucho para que te salga bien sin tener que recurrir a una explicación cada vez que lo intentes. Para ello solo debes recordar los puntos básicos que te hemos explicado en cada operación. Además, la práctica te llevará a que resolver operaciones con fracciones no te lleve tanto tiempo, lo que es ideal sobre todo en el caso de resolver exámenes.


muy buena información muchas gracias
Es una porquería yo esperaba la operacion de fracciones mixtas .II.