Rectas Tangentes – Qué son y Significado
Contenido del Artículo
Las rectas tangentes forman parte de la geometría. Es un elemento básico de esta parte de las matemáticas. Puede que hayas comenzado a estudiar en el colegio este concepto y estés algo perdido. Si ese es tu caso no te preocupes. En este artículo vamos a explicarte de la manera más sencilla posible qué son las rectas tangentes. Y cuál es su significado. Si estás interesado en conocer más datos… ¡no esperes más para seguir leyendo!
Qué son las rectas tangentes. Cuál es su significado
La definición más básica de una recta tangente podría ser la siguiente. Una recta es tangente a una curva cuando la toca en un solo punto y no la corta.
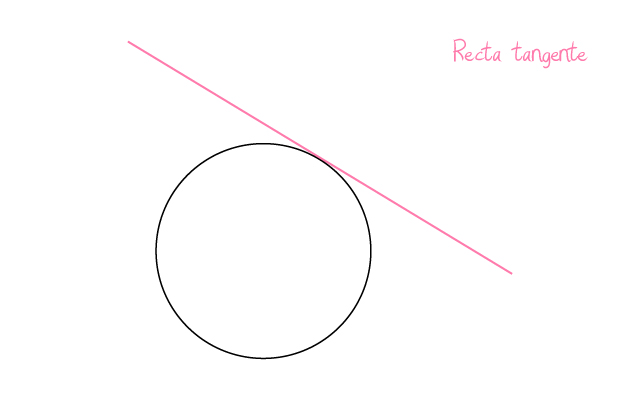
Si te fijas en esta definición se mencionan varios términos que resultan muy importantes para poder comprender qué son las rectas tangentes. El primero de estos términos es la palabra recta. El siguiente es la palabra curva.
¿Qué es una recta?
Cuando hablamos de una recta, ¿qué queremos decir? Una recta, o mejor dicho, una línea recta, está compuesta por un número infinito de puntos que se extiende en una misma dirección. Al extenderse en una dirección tienen también una única dimensión. Si aproximáramos una lupa hasta la recta que nosotros vemos veríamos que esta compuestos por muchísimos puntos pequeñitos que no tienen fin.
Seguramente al leer esto alguno se preguntará “¿cómo que un número infinito de puntos?” Sí, un número infinito ¡nunca se acaba! Si no fuese así estaríamos hablando de otros elementos de la geometría. Por ejemplo por un lado
- Semirrectas. Al hablar de semirrectas nos referimos a aquellas líneas que tienen un punto origen pero carecen de un punto con el que finalizan su recorrido. Es decir, que su otro extremo se extiende hasta el infinito.
- Segmentos. Cuando hablamos de un segmento nos estamos refiriendo a una línea recta que está delimitada por dos puntos. Uno de inicio y uno de fin. Muchas personas cuando comienzan a estudiar geometría confunden los segmentos con las rectas. Esto sucede porque, si lo piensas, no podemos representar visualmente una recta. ¡No acaba nunca! El profesor cuando lo explica crea en la pizarra una línea recta que verdaderamente tiene un final y un principio. Es decir, un segmento. De ahí vienen la confusión pues hay que echarle imaginación a la explicación del profesor y pensar que estas líneas nunca se acaban.
Ahora que hemos entendido un poco mejor qué es una recta, echemos un vistazo rápido a la ecuación general de una recta.
La ecuación general de una recta está dada por la siguiente expresión: Ax + By + C = 0.
En esta ecuación los valores A, B y C pertenecen al conjunto de números reales. ¿Sabes qué son los números reales? Los números reales se dividen en números racionales e irracionales. Los racionales son las fracciones de un número entre otro. Mientras que los irracionales son todos los demás números. Pero volvamos a la ecuación general de una recta. Mientras que los valores A, B y C pertenecen al conjunto de números reales, por su parte el valor B siempre es distinto de 0.
Partiendo de esa ecuación podemos aprender a despejar la «y» con lo que tendríamos:
By =-A x – C –> y = – A / Bx – C / B
Esta otra forma de expresar la misma ecuación nos permite ver claramente que la pendiente de una recta sería – A / B y la ordenada en el origen sería – C / B.
Con esta información podemos dibujar o representar cualquier recta en el plano cartesiano. Los planos cartesianos son aquellos planos que tienen dos coordenadas. La coordenada X y la coordenada Y. La coordenada X se suele dibujar de manera horizontal y la coordenada Y de manera vertical. Estas coordenadas forman un ángulo de 90º entre ellos y también son conocidas como ejes. Si dos rectas forman un ángulo de 90º grados, ¿cómo son en relación la una a la otra? Perpendiculares.
¿Qué es una curva?
Otro de los conceptos importantes que hemos mencionado es la curva. No olvides que hemos explicado que una recta tangente es aquella que tiene un único punto en común con una línea curva pero no la corta. Es decir, que se toca en un punto.
Pues bien, ¿Qué es la línea curva? La línea curva resulta muy parecida a la recta, ya que compuesta por una línea continua que se forma por un número infinito de puntos. Pero ojo:
- Tendrá un número infinito de puntos cuando hablamos de curvas abiertas, como la parábola.
- Sin embargo puede tener un número finito de puntos (como sucedía con los segmentos o semirrectas en las líneas rectas) y no seguir la misma dirección. En ese caso hablamos de curvas cerradas. ¿Se te ocurre un ejemplo de curva cerrada? ¡Efectivamente! Un buen ejemplo de curva cerrada es el círculo. ¿Se te ocurre otro ejemplo de curva cerrada? ¡La elipse! La proyección de la Tierra sobre un plano sería una elipse. Recuerda que el planeta Tierra no es redondo del todo.
![elipse]()
La ecuación de una curva es mucho más complicada que la de una línea recta. No te preocupes, te la vamos a explicar de manera muy sencilla para que puedas comprenderla. En términos generales podríamos decir que para obtener una ecuación lo que se hace es descomponer la curva en tantos segmentos como sea necesario y definir ecuaciones para cada uno de ellos que cumplan lo siguiente:
La ecuación entre el punto A y B: (A<T<B ) sería:
x=f1(t), y=f2(t), z= f3(t)
Finalmente vamos a intentar expresar matemáticamente una tangente de la forma más sencilla posible.
Si nos imaginamos un círculo de radio uno, cuyo centro está en el origen de coordenadas de un sistema cartesiano, y dibujamos una línea recta que pasa por el origen de coordenadas y corta al círculo en un punto cualquiera del cuadrante positivo, obtendremos un ángulo Alpha entre el eje x y la recta. Y si proyectamos hacia el eje x el punto donde la recta corta a la circunferencia obtendremos un segmento AB. Igualmente si proyectamos hacia la recta que hemos dibujado el punto donde la circunferencia corta al eje de coordenadas X, obtendremos el segmento CD.
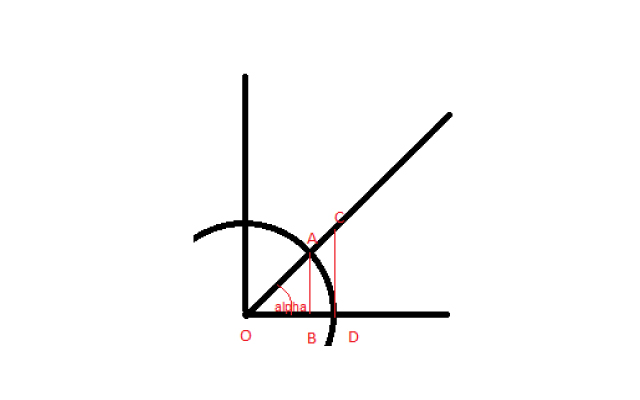
Aplicando la trigonometría, que se basa en la medición de los triángulos, sabemos que la tangente es la razón entre el cateto opuesto y el adyacente, en este caso
Tan (alpha) = AB / OB = CD / OD.
Dado que el radio de la circunferencia (OD) era 1:
Tan (alpha) = CD.
Hagamos un ejercicio para averiguar si hemos comprendido qué son las rectas tangentes
Bien, ahora que ya hemos terminado de explicar el significado de rectas tangentes queremos proponeros un ejercicio para averiguar si habéis comprendido bien cuáles son estas rectas. ¡Vamos a ello!
Esta tarde Paquito ha ido con sus padres al circo. El circo está un poco alejado de su casa, así que han ido en tren hasta allí. Se trata de uno de los espectáculos que más le gustan a Paquito. Le encanta divertirse con los equilibristas, ver a los payasos y observar lo grandes que son los elefantes. Mientras están sentados en las gradas Paquito observa todo lo que le rodea. Su padre sabe que ha empezado a aprender en la escuela los principios de la geometría. El mundo de las rectas ya no es algo desconocido para Paquito y parece divertirle mucho. Por este motivo a su padre se le ha ocurrido una idea mientras esperan a que comience el espectáculo. ¡Buscar rectas de diferentes tipos tanto dentro como fuera del circo! ¿Te gustaría unirte al reto que ha propuesto su padre a Paquito? En ese caso te vamos a enseñar una serie de imágenes para que nos digas el tipo de rectas que ves en ellas. Veamos cuánto sabes sobre las rectas.

- Imagen 1. En esta imagen puedes ver las vías de un tren. Si te fijas estas vías están compuestas por raíles. ¿Qué relación tienen las dos líneas que forman los raíles? ¿Sabrías decir qué tipo de rectas son?
![ejercicio 1]()
- Imagen 2. En esta imagen vemos a un equilibrista que hace sus trucos malabares sobre la cuerda. En este caso el ejercicio que hace es verdaderamente difícil. No camino sobre sus pies, sino sobre una bicicleta. Las ruedas de la bicicleta tocan la cuerda. ¿Qué tipo de recta es esa cuerda en relación a las ruedas de la bici?
![ejercicio 2]()
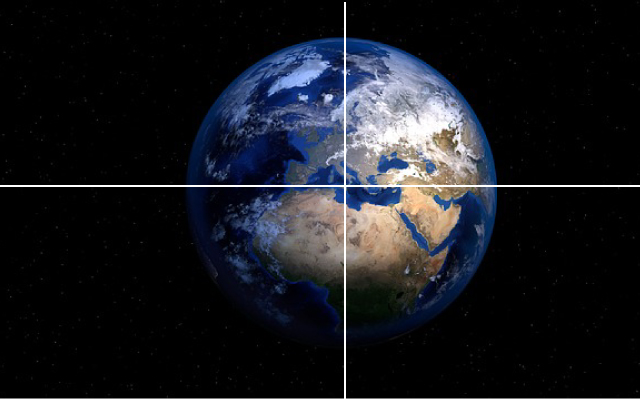
- Imagen 3. Aquí puedes disfrutar del planeta Tierra. Hemos marcado sobre él las líneas del horizonte y las de los polos. Las cuales atraviesan por completo la Tierra. ¿Qué relación tienen estas rectas entre sí?
![ejercicio 3]()
Solución
- Imagen 1. ¿Te gustan los trenes? ¿Has averiguado qué tipo de relación tienen las rectas que conforman los raíles? ¡Efectivamente! Se trata de rectas paralelas ya que no se tocan y tienen la misma pendiente.
- Imagen 2. ¡Qué gran equilibrio tiene este malabarista! Debe de ser verdaderamente difícil avanzar con una bicicleta sobre una cuerda. ¿Qué tipo de recta forma esta cuerda en relación con las ruedas de la bici? Se trata de una recta tangente ya que toca el círculo que forman las ruedas pero no lo atraviesan.
- Imagen 3. Si cortamos la Tierra en función de la línea del horizonte y los dos polos lo que nos encontramos son rectas perpendiculares. Estas se cortan entre sí formando 4 ángulos de 90º.
Si te ha gustado este artículo sobre las rectas tangentes…
Si has aprendido cosas nuevas e interesantes sobre las rectas tangentes, tanto sobre qué son y su significado, estamos seguros de que te encantará la sección de Matemáticas.
Dentro de esta sección encontrarás otros artículos interesantes relativos a la geometría, a la trigonometría y a las matemáticas en general. Aquí te dejamos algunos títulos con su respectivo enlace que pueden resultar de tu interés. ¡No dejes de echarles un vistazo!
Si te apetece compartir tus conocimientos sobre el interesante mundo de las rectas tangentes con nosotros y nuestros lectores puedes utilizar el apartado de comentarios. Lo encontrarás justo al final de este artículo. Prueba a colgar tus propias reflexiones sobre las rectas tangentes o incluso a crear ejercicios para poner a prueba a los demás lectores. Si tienes dudas también puedes resolverlas en este apartado. La comunidad de lectores de doncomos te ayudará a solventarlas sin problemas.
Si te ha gustado este artículo, ¡compártelo con nosotros! Dale al “si” y así sabremos que estamos realizando un buen trabajo. Los redactores aprendemos mucho con vuestros comentarios y vuestros likes. Nos ayudan a seguir mejorando.
Como siempre te damos las gracias por leernos. ¡Doncomos no existiría si no fuese por ti!